Dilimize Fransızca “perspectif”(bakış açısı)’ten gelen sözcüğün latince tabanı ‘per'(boydan boya), ‘specere’,’spect’ (gözlemek, bakmak) kelimelerinin birleşimiyle “perpektivus” “perspect”(boydan boya derinlemesine bakmak) olarak yer alıyor. Bu konuda derslerde verilen örnekler açısından en yetkin isimlerden İtalyan Carlo Crivelli’in “the annunciation” adlı resmi ya da Giorgio De Chirici resimlerinin bir çoğu olsa da, Alman ressam Albrecht Durer’in bu konudaki teknik kitapları ki perpektif için başlı başına kadrajı sağlayan ve gözü sabitleştiren bir makinası bile mevcuttu ve bu onun bilim arzusunun kanıtıdır ki bu anlamda teorik perspektifin endüstirileşmesine de olanak sağladı… (bkz: zograskop), (bkz: stereoskop)
 Albrecht Durer’in nü tablolarında kullanılmak üzere geliştirdiği Perspektif Makinası
Albrecht Durer’in nü tablolarında kullanılmak üzere geliştirdiği Perspektif Makinası
 Carla Crivelli’nin “The Annunciation” adlı resmi
Carla Crivelli’nin “The Annunciation” adlı resmi
Diğer yandan perspektif kurallarını altüst eden Maurits Cornelis Escher’in “Convex and Concave”, “Waterfall”, “Ascending and Descending” gibi resimlerinde perspektifin olanaksızlığa da kapı açabildiğini görüyoruz, Tıpkı Salvadore Dali’nin “Crucifixion” adlı resminde üç boyutlu perspektiften dört boyutlu perspektife geçişinde görülebileceği gibi.
 Escher’in “Ascending and Descending” adlı eseri
Escher’in “Ascending and Descending” adlı eseri
 Salvador Dali’nin “Crucifixion” adlı tablosu
Salvador Dali’nin “Crucifixion” adlı tablosu
Haritacılık içinde önemli olan perspektif bir yandan Batı’da boyut, sonsuzluk mesafe bilgisi olarak ele alınırken, Çin ve Japon sanatında “kuş bakışı” gözlemin ilke olarak edinildiği gözüküyor.
Bir çok mimari, 3d , 2d nesnelerin tasarımında kullanılan yazılımlar için gerekli olan perspektif bilgisinin ilk kaynaklarından biri mimari açıdan her ne kadar içgüdüsel hesaplamalarda olsa Antik Yunan’ın anıt mezarlarıdır. (bkz: parthenon). Daha sonra natüralizm etkisiyle işin içine rönesans mimarlarından Filippo Brunelleschei, Leon Battista Alberti ve ressam Piero Della Francesca ile perspektifin öncüsü olarak anılmasına sebebiyet verecek metodoloji sözkonusu olmuştur. Burada Arşimed’in ve Öklid Geometrisinin perspektife tutarlı kurallar getirmesi açısından önemi büyüktür. Zira, Leon Battista Alberti’nin 1435’teki “De Pictura” eserinde perspektifin geometri ve resim sanatını uygulayan bir yasal mimari yöntem olarak ele alması bu metodolojinin ilk sonuçlarıdır.
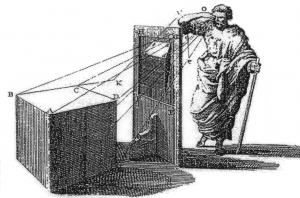 Alberti’nin çalışmaları mimari perspektif anlayışa yeni bir yön verdi.
Alberti’nin çalışmaları mimari perspektif anlayışa yeni bir yön verdi.
Rönesans döneminde matematikçiler cephesinde ise Fransız mimar ve geometri ustası bir matematikçi olan Girard Desarques”in “projektif geometri” kavramını ele alıp, temellendirmesinden ve sonrasında Hean Henri Lambert ve Gaspard Monge adlı matematikçilerin de bu temellerin kanıta dayalı ilişkilendirmelerini yapmadan yaklaşık 100 yıl öncesinde bir isim daha göze çarpar: İtalyan ressam, filozof, astronom Guidobaldo Del Monte’nin 1600 yılında yayınladığı “perspectivae libri vi” adlı eserinde getirdiği optik yanılma ve perspektif üzerine matematiksel tabanlı teorisidir.
 Perspektif ustası Leonardo Da Vinci’nin çizimlerinden biri
Perspektif ustası Leonardo Da Vinci’nin çizimlerinden biri
Perspektifin felsefeye etkisi ise; bilginin fenemonolojisine dair ve neokantçı görüşleriyle, ayrıca dil ve sembolik formlar felsefesi kitaplarından tanınan alman filozof Ernst Cassirer’in “Rönesans Felsefesinde Evren ve Birey” kitabında “Matematik, bir kavram ve estetik bir kategori olan orantı, araştırmacı ile yaratıcının, doğanın gizemlerini araştıran insanla, yaratıcı sanatçının buluştuğu noktadır.” diyerek perspektifin matematik temelleriyle sanattaki görüntüsüne kattığı gerçeklik ve estetik adına yüceltilmesi olarak yorumlanabilecek kadar önemlidir.