Gödel teoremi şöyle açiklanabilir:
Aksiyomlardan veya yöntemsel kurallardan veya benzerlerinden oluşan herhangi bir biçimsel matematik sistemi, aritmetik teoreminin tanimlamalarını kapsayacak kadar geniş kapsamli olmasıı ve çelişkisiz olmasi koşulu ile, sistemin kapsamına alınan yöntemlerle ne kanıtlanabilir ne de kanıtlanamaz bazı bildirimleri içermelidir. Buna göre bu gibi bildirimlerin doğruluğu hakkında, onaylı yöntemlerle karar verilemez.
Gödel, matematiğin hiçbir alanında tutarlılığın, o düzenin yöntemiyle ispatlanamayacağını ortaya koymuştur. Bunun için dizgenin dışından başka yöntemlere ihtiyaç vardır. öyle ki p gerçekten tutarlı ise, p’ nin tutarlılığı p’ nin terimleriyle oluşturulan bir ispatla ortaya koyulamaz. Tutarlılığa ait bu sonuç, Gödel’ in eksiklik teoremiyle birleştiğinde, Hilbert programının iki amacının ilk amacı olan tutarlılık ve tamlık’ ın gerçekleşme olanağı yoktur.
Gödel’ in eksiklik teoremine göre; tutarlı bir sistemin eksikliği ‘ herhangi tutarlı bir sistemde o sistemin ispatı verilemeyen düzgün bir formülü vardır‘ şeklinde açıklanabilir. bu teoreme göre aritmetik ölçüsünde kurulacak aksiyomatik dizge eksik kalmaktan kurtulamaz. hilbert, programının gerekçesini şu şekilde ortaya koyar:
“ Teorimin amacı , matematiksel yöntemlerin güvenirliğini bir daha tartışılmayacak bir kesinlikte ortaya koymaktı…kanımca bizi paradokslarla karşı karşıya bırakan şu sıradaki gelişmelere göz yumup geçemeyiz. doğruluk ve kesinliğin kalesi olarak bilinen matematikte herkesin öğrendiği, öğrettiği ve kullandığı tanımlarla dedüktif yöntemlerin yol açtığı saçmalıklara bir bakın. peki ,matematiksel düşünme böylesine kusurluysa , doğruluk ve kesinliği nerede bulacağız?” [david hilbert ” on the infınite” philosophy of mathematics]
‘mars ürünü’ sayılar yani gerçekte marslıların ders kitaplarında yer alan ifadeler denilebilecek şeyleri hayal ederek şu soruyu soralım: 2042985 mars ürünü mü yoksa değil mi? yani 2042985 ifadesiyle mars kitaplarında karşılaşacak mıyız? Gödel şöyle demiştir : “x bir mars-ürünü sayı değildir ifadesi mars matematiğine tercüme edildiğinde, x dünyada gerçekten bir sayı ise ‘x bir mars-ürünü sayı değildir, anlamina gelir. “X bir mars-ürünü sayı değildir” ifadesi bize uzun basamakli bir sayı gibi görünecektir ancak bu mars dilindeki yazım biçimi, ifadede sözü edilen bizim x sayımızın, sayısal biçimde ifade edilmiş haline karşılık gelecektir.
Teoremler, sembol kalıpları olarak düşünüldüğünde, biçimsel sistemdeki ifade yalnızca kendinden bahsetmez, aynı zamanda teoremin kendine de karşı gelebilir. Gödel, sınırlı aksiyom ve kurallarıyla matematiğin tüm doğrularını barındırmayı amaçlayan biçimsel sistemlerin tutarsızlığını göstermiştir. Biçimsel matematiksel sistem verilen bir matematiksel önerme ile ilgili simgeler dizisinin, sistem içerisinde bir kanıt oluşturup oluşturmadığına karar vermek işleminin ‘hesaplanabilir’ olmasını gerektirir. Önerilen bir kanıtın gerçekten bir kanıt olup olmadığını, tümüyle mekanik ve önceden belirlenmiş bir yöntemle kontrol etmek mümkün olmalıdır. Yani kanıtları kontrol eden bir algoritma bulunmalıdır. Bir biçimsel sistemde ne zaman bir kanıt varsa kanıtı bulmak için de daima bir algoritma vardır. Bir kanıtlar listesine sahip olduğumuzda, formel sistemin ‘tüm’ teoremlerine de sahip olmuş oluruz.
Hilbert, matematik sistemi kapsamında doğru formüle edilmiş herhangi bir matematik önermesinin doğruluğuna ya da yanlışlığına formel bir kanıtla karar vermemizi sağlayacak kadar güçlü bir aksiyomlar ve kurallar sistemi bulmayı başarsaydı, bu gibi önermelerin doğruluğuna karar verilmesini sağlayacak genel bir algoritmik yönteme sahip olacaktık. Böylece, mekanik yöntemimiz herhangi bir aşamada daima son bulacak ve biz de sistemin tüm önermelerinin doğruluğu ya da yanlışlığı hakkında kara vermemizi sağlayan evrensel bir algoritmaya sahip olacaktık. Oysa bu durumda, turing’ in matematik önermelerle ilgili karar vermeyi sağlayan genel bir algoritmanın var olmadığına dair bulduğu sonucun aksi kanıtlanmış olacaktı.
Turing makinelerinin(bkz: turing makinesi) durup durmamasına ilişkin karar verebilecek hiçbir algoritmanın var olmadığını göstermekle Turing, matematik önermelerle ilgili karar vermenin genel algoritmasının bulunmadığını göstermiştir. Bu da genel nitelikte, iyi tanımlanmış tüm matematik problemlerini çözümlemesi için algoritmik bir yönteme ihtiyaç duyan hilbert probleminin çözümsüzlüğü demektir.
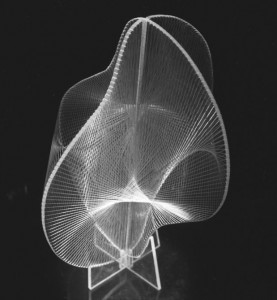Uzayın derinliklerini tarayan dev bir radyoteleskopun bir anıta dönüşümünü Rotterdam kentine diktiği çelik, cam ve pleksiglas “Kurulmuş Heykel” adlı yapıtta bulabileceğiniz, eserlerinde yüksek matematik modellemeleri kullanan, Rusya’da doğup Amerika’da 70 lerin sonuna doğru ölen, teknolojinin insanoğlunun başarısı içinde anlam kazandığını düşünen, konstrüktivist, kinetic art temsilcisi dahi heykeltraş sanatçısı…
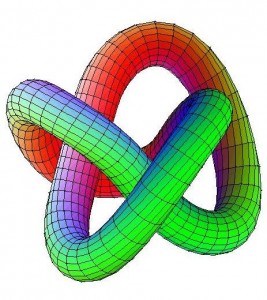
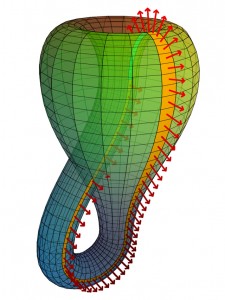Felix Klein’ın ünlü imkansızlık abidesi,topolojik uzay nesnesi…Gözümüz açısından yani 3d bazda yer bulamayan ama 4d ortamda süreksizliği anlatan bu şekil, aynı zamanda Escher gibi bir ressama da tıpkı “Mobius Şeridi” gibi “çiz beni” dedirttiği gibi, anonim şiirlere ve bulmacalara da ilham vermiştir.
