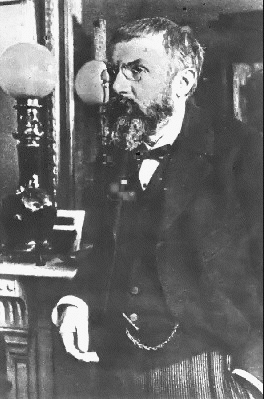”Bilim gerçeklerden kuruludur,tıpkı evin tuğlalardan kurulu olması gibi.
Ancak gerçeklerin toplanması bilim değildir.Tıpkı bir küme tuğlanın ev anlamına gelmemesi gibi.”
/Henri Poincare
Bir Fransız matematikçisi olan Henri Poincare 1854 yılında Nancy’de doğmuştur. yüksek öğrenimini Polyechnique’de yapmıştır.
Üniversite mezuniyeti sonrası O’nun ilk yaptığı iş Maden Ocakları Birliği’nde bir çeşit mühendislik hizmetidiri. Ancak kısa sürede akademik yaşamı yeğleyecek ve bu göreve Sorbonne Üniversitesi’nde başlayacaktır. Bütün akademik yaşamı sadece bu üniversitede sürmüştür. Bilimsel çalışmalarının yanında hiç aksatmadan sürdürdüğü ders görevleri de vardır. Bu sabır isteyen çalışmaları sonrası, irili ufaklı beşyüz civarında eser vermiştir. Bu sayı belki de matematik tarihinde adı geçen bunca bilginin çalışmalarının çok çok üstünde bulunmaktadır. Çoğu makale ve bildiridir ve hemen tamamına yakını yayımlanmıştır. Aralarında kitaplar da bulunmaktadır ki bu çalışmalardan önemli bulunan bazıları aşağda tanıtılacaktır.
O’nun çalışma konuları daha çok analitik fonksiyonlar, diferansiyel denklemler ve özellikle cebirsel geometri olarak ağırlık kazanmaktadır. ilerideki yıllarda bilim felsefesi ile de ilgilenmiştir. bizim yaklaşımım, O’nun geometriye ilişkin çalışmalarını biraz daha önce çıkarmak olacaktır. Ancak daha önce diğer konulardaki çalışmalarına şöylece değinmekte yarar vardır.
Diferansiyel denklemlerle olan ilgisi daha çok gök mekaniği ve üç cisim porblemleriyle uğraşırken karşılaştığı bir model olması enedeniyle başlamıştır. Benzer şekilde kısmi türevli diferansiyel denklemlere de matematiksel fizik” çalışmaları sırasında ilgi duyacaktır. Bu çalışmaları sırasında iki tür diferansiyel denkele de kendince katkılarda bulunmuştur.
O’nu matematikte en çok etkileyen süreklilik kavramı olmuştur. Bütün çalışmalarında bu düşünce, O’nu yönlendirmiştir. Buna koşut olarak topolojij türden bir çok problemle uğraşmıştır. Giderek bu birikim, O’nun Cebirsel Topoloji’yi kurması aşamasına kadar uzanacaktır.
Bir süre kümeler ile ilgilenecek, karşılaşılan bazı paradoslar nedeniyle biçimcilerle çatışacaktır. Bu davranışlarıyla bir kaç meslektaşlarıyla ters düşmüş bile olsa, O daha çok sezgici görüşü benimseyen tarafta yer almıştır.
“Matematiksel Fizik” konusundaki çalışmalarının ardından ” Bilim Felsefesi” ne yönelecek ve özellikle bu konuda çeşitli dersler verecektir .Akademik yaşamına devam ederken, 1887 yılında bilimler Akademisi’ne 1908 yılında ise Fransız Bilim Akademisi’ne üye kabul edilecektir.
Tam bu yıllarda, yüzlerce çalışması arasına üç kitap yerleştirmiştir. Bu kitaplar, yayımlandıkları yıllar itibariyle şunlardır:
-Bilim ve Varsayım -1902
-Bilimin Değeri-1906
-Bilim ve MEtod- 1909
20. yy’a girilirken Henri Poncare adı, artık bilinen ve tanınan ve de bir otorite olarak kabul edilen bir adır. Artık O, göz kamaştırıcı bir şöhrete sahiptir. Yaşamının son yıllarında prostatı ile başı derttedir. 1912 yılının ilk baharında bir ameliyat geçirecek, ancak bu ameliyat sonrası oluşan bir amboli nedeni ile 17 Temmuz 1912 günü yaşama veda edecektir. 59 yaşında, Paris’te ölmüştür.
Henri Poncare’nin yaşam öyküsü böylece özetlenebilir. Ancak O’nun çalışmaları ve fikirleriyle matematiğe yaptığı katkılar hakkında elbette bir şeyler söylenmelidir.
x1,x2,x3,x4 projektif koordinatlarının x1′,x2′,x3′,x4′ lerle olan bağlılıklarının lineer olmaması halini inceleyen Cremona ve O’ndan sonra da Bertini, CEbirsel Geometri adı verilen yeni bir geometri icad etmişlerdir. Cremona transformasyonlarına birasyonel transformasyonlar denilmektedir. Bunlar bir grup oluşturmaktadırlar. Cebirsel Geometri, bu Cremona Grubu’nun geometrisidir.
Bu saydıklarımızdan başka, daha yeni bir geometri vardır ki en iyi matematikçileri bile hayli düşündürecektir. Bu disiplin, Analysis Situs adıyla ortaya atılan ve sonra da Topoloji olan bir konudur. Bu konuyu az çok tanıyoruz. Bu çeşit geometrinin, geometrik varlıkların ölçüsü ve büyüklüğü ile hiç ilgilenmeyen ve ortak kalitatif özelliklerinden söz eden bir disiplin olduğu görülmüştür.
Bu fikri, ilk kez Geometria Situs adıyla ortaya atan Leibniz’dir. Çünkü, O matematik analizin tümüyle doğa felsefesinin bütün sorunlarına yanıt verecek derecede yeterli olacağına inanmıyordu. bu görüşünü O, Paris Bilimler Akademisi 1771 yılı dergisinde yayımlanmıştı.
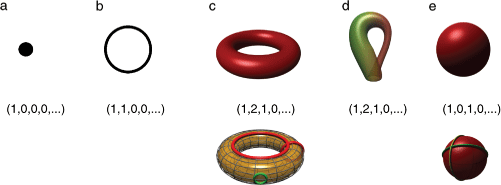
Topolojide geniş bir soyutlama fikri egemen olduğundan ,onun problemlerini kavramkta güçlük çekilebilecektir. Henri Poincare matematiğin bu konusunun ilerlemesinde oldukça katkıda bulunacak ve özellikle de çok boyutlu bir baryetenin tanımlanabilmesi için Betti Sayıları denilen bir takım büyüklüklerin bilinmesine gereksinme vardır.
Enrico Betti, bir İtalyan matematikçisidir. O riemann çizgisinde matematik yapan biriydi ve bundan esinlenerek O, aşırı uzayların bağlantı düzeni üzerine ünlü olan bir inceleme yayımlayacaktır. 1871 yılında yayımlanan bu makalede ” bir katlı uzayın bağlantısını belirten Betti Sayıları” tanımlanmaktadır. İşte bu sayılar Poincare’ye ilham vermi şve O kanıtlamıştır ki böyle her sayı sistemine, biri diğerine deforme olmayan , sonsuz bir varyete karşılık gelecektir. Poincare bu şekilde hareket ederek, çok yüzlüler için önceden bilinen Euler teoremini genelleştirmiştir. Bu konuda, Euler’den söz ederken yeterince bilgi verilmiştir. Orada ifade edilmiştir ki Euler, üç büyüklük(köşe sayısı, ayırt sayısı,yüzlerin sayısı) arasındaki bağıntıyı kuracaktır. buradan bir yolla bu yüzeylerin değişimi fikri O’nları topoloji kavramına kadar götürecektir. İşte görülüyor ki H.Poincare’nin uğraş verdiği konunun öncesi Euler’e kadar gitmektedir.
Henri Poncare’nin pek çok matematikçide görülmeyen bir ayrıcalığı vardır ki o da matematikte estetik fikrini ciddiye almasıdır. Bu konuda özellikle matematik kafasının belirleyici niteliği hakkında O’nun görüşü bazı çevrelerce ilgi ile karşılanmıştır. O Görmüştür ki, “matematik kafasını belirleyici şeyin mantıkla titizlikle veya cebirsel formüllerle işlem yapabilmekte ve hatta kat kat soyutlamaların ustalıkla üstesinden gelme yetisiyle belki de fazla bir ilişkisi yoktur. Henri Poincare’nin anıtsal yazıları sadece matematikçileri değil çok geniş bir entellektüel çevreyi de ilgilendirmektedir. O bütün bu yazılarında bir ana fikirden hareket ediyordu: “matematiğe karşı bir estetik duyarlılık, matematikçinin ruhunu belirlemektedir.” O’na göre bu duyarlılık, yaratıcı bir ruh için en önemli esin kaynağıydı.
Bunu en iyi tartıştığı yer, Bilim ve Yöntem(Science and Method) adlı eserinin “Matematiksel Yaratıcılık” için ayırdığı bölümünde bulunmaktadır. ORada ileri sürdüğü düşüncesine göre kişinin mantıktaki ustalığı ve matematiksel sembolerle iş görme yetisi ne kadar güçlü olursa olsun, matematiksel yaratıcılık için ayrıca sezgi erki de bulunması gerekmektedir. O, bu konularda bakın neler söylenmiş:
“Yaratmak, tam anlamıyla, yararsız düzenlemeler(kombinasyonlar) yapmamak, yararlı olan ve sadece küçük bir azınlık oluşturan düzenlemeler yapmaktadır. Keşif bir ayırt etme işi, bir seçmedir. yararlı düzenlemeler en güzel olanların ta kendileridir. Şunu demek istiyorum ki, bütün matematikçilerin bildiği sıradan insanların ise çoğu kez alaya alacak ölçüde habersiz oldukları bu özel duyarlılığı en iyi uyandıranlar bu düzenlemelerdir.”
Poincare’nin matematiksel sezgi diye nitelediği kavrayış, alışılmış anlamdaki normal bir akılcılığın dışındadır,o ancak yavaş yavaş ortaya çıkacaktır.
Poincare’nin yukarıda sözü edilen duyarlılık hakkındaki görüşü, bunun “doğuştan olduğu” doğrultusundadır. O’na göre bu duyarlılığa, görece çok az kişi sahiptir. Bu konuda şöyle demiştir:
“biliyoruz ki bu duyguyu, bize gizli duyumları ve ilişkileri hissettiren bu matematiksel düzen sezgisine , herkes sahip olamaz. Kimileri, ne tanımlaması zor olan bu ince duyguya , ne de normalin üstünde bir bellek ve dikkat gücüne sahiptir. Bu kişilerin yüksek matematiği anlamaları kesinlikle olanaksızdır ve çoğunluk da bu durumdadır.”
Poincare’nin yaklaşık yüzyıl önce yazdığı bu satırlarda anlatmak istediğini günümüze uyarlamak da olanaklıdır. O’na göre sıradan insanlar büyük çoğunluktadır ve matematiğin estetiğine duyarlı olmak ayrıcalığı, olsa olsa halkın az bir kısmına verilmiştir ki yaratıcı matematikçiler işte bunlar arasından çıkacaktır. Bu görüş, estetik duyarlılığın doğuştan geldiğine inanan kimseler tarafından benimsenmiştir. Bu görüşe göre ” eğer sizde varsa ,sizde onlardan biri olursunuz, eğer yoksa sizin için yapılacak bir şey yoktur.”
Poincare bu gibi düşüncelerden yola çıkarak, matematiğin pek de önemsenmeyen ya da üzerinde fazlaca durulmayan bir yönüne ışık tutmaktadır. Matematiğin hem estetik yönünü öne çıkarmak hem de bununla yaratıcı kişilik arasında bağlar kurarak matematikçiyi nitelemek,olsa olsa “matematikçiyi” tanımlarken kullanmak istediği bir kriter olarak düşünebilecektir.O’nun kullandığı gerçek matematikçi deyimi ile tanıtmak istediği, araştırmacı matematikçidir.
O’nun bu konudaki görüşlerini matematik eğitimi için uyarlanmaya çalışan bir başka bilimadamı Seymore A. Papert, “Matematiksel Bilinç-dışı” adlı makalesinde şöyle bir deyim kullanıyordu:.”Poincare’nin bu projesini yeryüzüne indirme! ” bununla da şunu anlatmak istemektedir. bu görüş ve anlayış, matematik öğretimine ve ğerinimine uygulanabilecek şekilde genişletilmelidir.
1978 yılında ortaya çıkan bu yartışma, Massachussetts Institue of Technology (Massachussetts Teknoloji Enstitüsü) üyesi olan S.A. PApert’in sayesinde çağımız içine çekilmiş ve Poincare’nin bu görüş ve yaklaşımları neredeyse güncelleştirilmiştir. Papert’e göre, matematiğin yıkıcı sonuçları ;”Poincare’nin, önemsiz sayılsa da, bu konuda bir paradoksa dönüştürdüğünü göstermektedir. Bu ise paradoksların gücünü anlamanın ta kendisidir. “Poincare’nin Bilim ve Yöntem kitabında şöyle yazılıdır:
” Dikkatinizden kaçan küçücük sebeplerden biri, görmekte ihmalkar davrandığımız öylesine büyük bir sonuca neden olur ki, biz de kalkıp bu sonucu tesadüfen ortaya çıktığını söyleriz. Doğanın yasalarını ve evrenin başlangıç anındaki durumunu tam olarak bilebilseydik, evrenin başlangıç durumunu izleyen daha sonraki anlardan birindeh angi durumda olacağını da tam olarak öngörmemiz mümkün olabilirdi. Doğa yasalarının artık bizden kaçıracak hiçbir sırrı kalmamış olsa bile gerçek durum hakkında yaklaşık olarak bilgi sahibi olabilirdik. bu sayede, başlangıç durumunu izleyen durumu aynı şekilde yaklaşık değerler olarak öngörmemiz mümkün olsa bütün istediğimiz gerçekleşmiş olur ve biz de bu fenomenin öngörülmüş olduğunu, yasalara uygun olarak cereyan ettiğini söyleriz. Ne var ki, her zaman böyle olmamaktadır; başlangıç sartlarındaki küçük farkların nihai olgularda çok büyük farklar meydana getirdiği de görülmektedir. Başlangıç şartlarındaki küçücük bir hata nihai olguda muazzam bir hataya neden olacaktır. Bu durumda olacağı öngörmek mümkün olamaz…” Kaos da Poincare’e göre böyle başlar ya da varolmaz veyahut hiç varolmamıştır.
O’nun son olarak bir başka çalışması ise anımsanacağı gibi, Öklidyen Olmayan Geometriler incelenirken, burada oluşan teorilerin evrenin olgularına çok daha doğru açıklamalar getirdiği görülmüştür. Bu demektir ki, bu geometrilerin herbiri değişik dünyaları betimlemede birer araç olarak kullanılacaktır. İşte bu,” değişik dünyalar” dan biri de Henri Poincare tarafından tasarlanmış ve tanımlanmıştır.
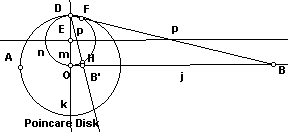
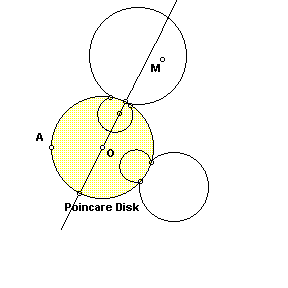
O’nun düşsel evreni, merkezinde sıcaklığın 0 Derece olduğu bir daireyle(üç boyutlu düşünüldüğünde bir küre) belirlenmiştir. Merkezden uzaklaştıkça , çevredeki sıcaklık artar. Bu evrendeki nesnelerin ve yaşayan varlıkların sıcaklık değişikliklerinden habersiz oldukları, her şeyin büyüklüğünün hareket ettikçe değiştiğini varsayalım. Her nesne ve canlı, merkeze yaklaştıkça büyür; merkezden uzaklaşıp sınırlara doğru yaklaştıkça orantılı olarak küçülür. Her şeyin büyüklüğü değiştiği için kimse büyüklüklerin değiştiğini farkedemeyecek ve bundan haberi olmayacaktır. Herhangi birinin admları sınırlara yaklaştıkça küçülecek ve sanki sınıra hiç yaklaşıyormuş gibi görünecektir. Dolayısıyla bu dünya, sonsuzmuş gibi görünecektir.
Bu” düşsel dünyada(evrende” iki nokta arasındaki en kısa yol bir eğridir. Çünkü A’dan B’ye gitmek için merkeze doğru bir yay biçiminde ilerlesek daha az adım atarız.(adımlarımız daha büyük olacağı için) Bu dünyadaki herhangi bir üçgenin kenarları şekildeki ABC üçgeninde olduğu gibi, yaylardan oluşmuştur. Paralel doğrular bile farklı görünecektir. Hiç bir zaman kesişmeyecekleri için DCE doğrusu AB doğrusuna paraleldir.
O’nun bu gibi düşünceleri, hiç kuşku yok ki 20. yy. matematiğini yönlendirmede çok etkili olmuştur. Deterministik(genlerle belirli) Kaos kavramını ilk keşfeden olarak bir anlamda Newton’un Güneş Sistemi’ndeki Kaos’undaki yetersiz kavramının bir ötesine geçmiştir. Poincare’nin dediği gibi “Ben bunun doğru olması gerektiğini biliyorum, o halde ne diye ispat edeyim ki?”